数学是从生孕育发生活中诞生的，随着数学的进展，渐渐凌驾了人们的想象。虚数便是数学进展历程中的一个典范例子，不外，直到今日，仍有许多小同伴对虚数表现难以了解。本文，就与您一路来聊聊虚数实在不虚。

一、实际中不该该存在的数

假设有一块边长为5米的正方形地皮，如今想把这个地皮扩大出39平方米而且照旧是正方形。实在这个标题很简洁，初中生应该都市，便是求方程（5+x）^2=25+39的根。最终得到的效果是x=3或x=-13。依据题意，可以得到x=3，由于边长不克不及是负数，以是-13是无效解。

假如前面这个例子还可以了解，那么下面这个方程就无法担当了。x^2+2x+2=0，为了求解x我们把方程变更一下(x+1)^2=-1。很显着，这个标题假如在实数范畴内是做不下去的。什么数的平方会是负数呢？

这个平方后能孕育发生负数的方程曾经在很长一段时间里困扰着数学家们，莱布尼兹就曾经以为，这是数学剖析中的一个奇怪，在实际中的是不存在的，以是就把它称作了虚数。

二、实际中的虚数意义

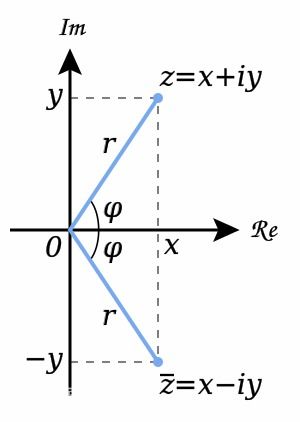
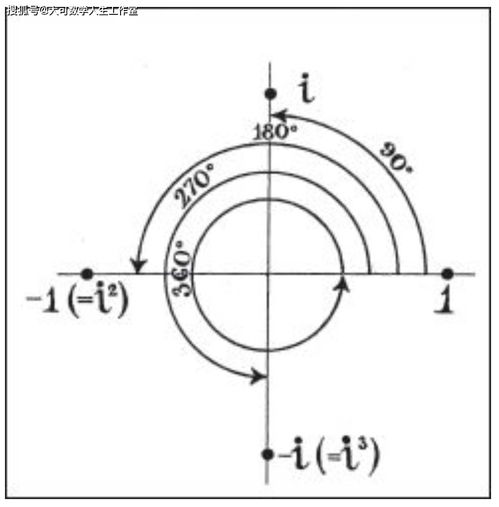
我们如今知道-1的平方根是i，让我们一路来探究一下i的性子。思量在一根数轴上的实数，1、2、3……，假如把它们乘以-1就得到-1、-2、-3……。这些数相称于是本来谁人数以原点为中间扭转180度。因为i^2=-1，这意味着，一个数两次乘以i扭转了180度。

换句话说，便是一个实数假如乘以一个i意味着扭转了90度。我们把一个实数乘以i之后的数叫做纯虚数，它位于与实数轴垂直的虚数轴上。方程x^2-6x+25=0有两个根，x=3±4i，这两个根便是在由实数数轴，以及与实数数轴垂直的虚数数轴构建的平面上的两个点相对应。我们把实数+实数i这种布局的数叫做复数。

很显着，复数的这个特点意味着这是一个逾越了只有正负两个偏向的实数，是一个能形貌平面上全部点的偏向的更广义上的数。虚数i的意义就在于与实数一路构建了一个向量空间，复数形貌了这个空间中的点间隔原点的间隔和脱离实数正偏向所偏转的角度。

对付一个复数z=a+bi，其间隔原点的间隔为r=（a^2+b^2）^(1/2)，其偏转角度为θ，tanθ=b/a。r被称为z的肯定值，用|z|来表现，θ叫做 z的辐角，用arcz表现。

三、虚数（复数）与物理学

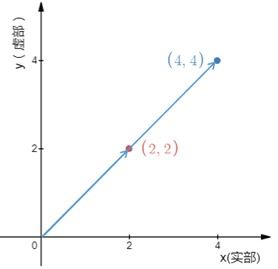
物理学中每每要盘算质点的位移，有了复数这种处置惩罚就简洁了许多。举个例子，某质点在t1时候其复平面内的位置为r1=2+3i，t2时候的位置为r2=5+3i，求t1、t2时候中位移的改变Δr。实在也很简洁，r2-r1=3。意味着，在这个时候内，这个质点沿着实数轴的正偏向移动了3个单元，而在虚数轴正偏向位置连结稳定。

因为不是数学内容，以是这里简洁总结一下复数运算的物理意义。复数的加减法实在便是分别沿着实数轴和虚数轴的平移，而复数的乘除法实在便是复数的伸缩和扭转。正是由于复数的这种性子，以是复数很天然地被应用于物理学当中。

在GPS导航中，复数被用于盘算和形貌交通东西所处的位置及位置改变信息。因为复数不但有巨细（间隔）并且还包罗辐角，以是也被用于形貌许多周期性的改变活动当中，尤其是在电磁学当中有着非常遍及的应用，厥后更被应用于量子力学当中。

现在，复变函数是物理专业门生的根本盘算技能，是物理系本科生，数学科目中的必修课。

完结语

虚数的应用另有许多，本文只是点到为止。我们必要记着的是，从数的角度来说，虚数拓展了数的空间，办理了许多高次方程的数学解的意义题目，并且还能办理许多多少题目。固然了，从物理的角度来说，它与实数一路构建了一个可以或许形貌空间恣意点的间隔和偏向的复数空间。任何与间隔和偏向有关的量都可以用复数来表现，而这正是物理要办理的根本题目。

很明显，虚数不“虚”，小同伴们，你们GET到这个点了吗？关于虚数另有哪些现实应用，接待鄙人面的留言区中批评参加。

文/郭哥聊科学 图片来自网络侵删。