小乐数教科普：怎样使用柱面坐标盘算三重积分，比方曲面所围体积

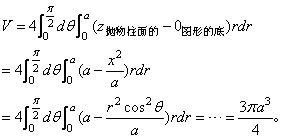
盘算线、面、体的积分是微积分学科中的重难点之一，也是理工科大门生需把握的焦点知识点之一。本文小乐通过一个详细案例，给出典范求解重积分的要领历程，并在此中每一步调，给出相应道理解说与相干的扩充知识点，供家人们体系进修或温习时参考。

起首，我们给出原题：

使用三重积分盘算下列由曲面所围成的立体的体积：

求曲面所围成的立体的体积

拿到这道题，我们必要先阐发一下，题中用方程表现出来的这两个曲面，分别是什么形状。

依据第一个曲面方程：

上半球面

明显这个方程，通过得当变形，易知表现球体的上半球面（球心恰好位于直角坐标系原点，球体半径为根号5）。

上半球面

而依据第2个曲面方程：

扭转抛物面

假如我们纰漏y大概纰漏x，就会发觉是抛物线方程（极点在原点，开口向上，即z轴正向），再依据x,y的对称性，易知这个方程表现一个扭转抛物面，可以当作一个极点恰好在原点，开口向上（z轴正偏向）的一条抛物线，绕z轴扭转一周后，得到的曲面。

扭转抛物面

那么这两个面相交后，明显我们可以联立方程组：

联立曲面方程组，求出解

得当变形解出方程组

解出：z=1，也便是说，这两个曲面相交于z=1的高度，相交的形状是一个圆。

曲面相交于z=1

那么我们可以将这两个曲面所围成的立体，沿着z=1，一分为二得到上下两部门，分块盘算体积。

所围立体一分为二

盘算三重积分

在上述第2步，我们将笛卡尔直角坐标系中的积分，变更成柱坐标系的积分。这里必要细致，被积函数必要乘以一个雅可比行列式（即是r），即下表中的第三个：

变量代换的雅可比行列式

然后在第3步，我们马上将重积分，化成累次积分（细致界定好各变量的上下限）。

固然这一题，如不限定利用柱坐标系盘算体积的话，我们实在可以利用劈面积微元举行积分（z从0到1，再从1到根号5）求体积的头脑，即对一层层薄单方面积存加求体积，详细一点便是把立体切成圆形薄片（与z轴垂直），每个薄片的面积都可以利用圆面积公式S=πr²，这里r随着z而改变，是关于z的函数，即：

面积元薄片

然后劈面积元举行一维积分，这就与上述第4步所得款式完全同等，但盘算速率更快，了解起来也不算太庞大，不失为一种查验原解答精确与否的要领，感谢你的阅读。